The POWER function in Excel is a very basic and easy-to-use function. It can readily execute fundamental mathematical exponential calculations on its own. However, when nested inside a complicated mathematical equation, the POWER function may help to minimize the size of otherwise highly complex formulas. Considering its simplicity, the POWER function is quite flexible. Users may compress various complex mathematical formulas using the function’s shorthand operator. In addition, it can show figures in scientific notation, create complex graphs and charts, and conduct geographic calculations. Knowledge of the POWER function is essential for individuals working with complicated mathematical data.
What’s Excel’s POWER Function?
POWER is a straightforward function that converts a given number to an exponent. The exponent might be a constant number or a reference to any cell in your workbook. In addition, the POWER function’s exponent argument may be either a positive or a negative number. Positive exponents are used for working with big numbers when expressing scientific notation, and negative exponents are used for working with tiny numbers.
The function features a shorthand, the circumflex operator, ^, and the regular POWER keyword. When employed in a formula, the circumflex operator does the same calculation as POWER. The number you are raising and the exponent you are raising to are the two parameters accepted by the POWER function. A sequence of multiplications may also be used to represent the POWER function. The two formulas below will produce the same results.
=POWER(5, 3)=5*5*5Multiplying any number by itself repeatedly produces the same result as the POWER function or its shorthand operator, but in most cases, using the function is significantly more readable. The first argument may be any real number supplied as a fixed number in the function or referenced from anywhere in the current workbook. The second argument’s exponent may be any real whole number, positive or negative.
How To Use Excel’s POWER Function?
In either version, the POWER function may be used on its own. It may also be nested within other functions to create more sophisticated mathematical formulas. The POWER function has the following syntax.
=POWER(number, power)“number” represents the base number, and “power” represents the exponent. So, for instance, we would write to increase the number 2 to the power of 3.
=POWER(2,3)The result of this calculation is 8.
=POWER(A2, 2)Any number entered into cell A2 will be squared, and the function will return the result. The same function might be written using the POWER function’s shorthand.
=A2^2When using the POWER operator rather than the function, the base is on the left side of the circumflex, and the exponent is on the right.
Using Excel’s POWER Function With Fixed And Arbitrary Powers
The number being raised may reference a cell in your current workbook, and the exponent can also be provided as a cell. The following function is created when the exponent is passed as a cell.
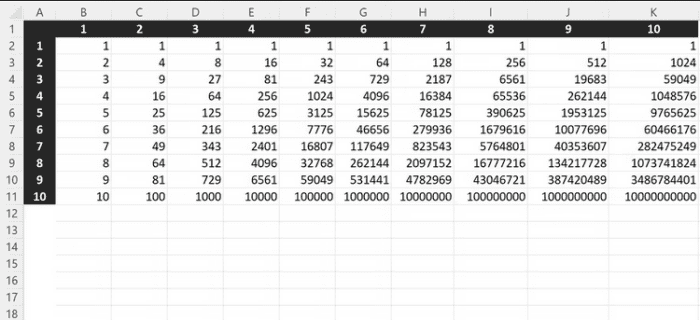
=POWER(15, A2)The results of the function mentioned above will be 15 to whatever power is entered into A2. We may create a basic power chart displaying a list of exponents using one of Excel’s array formulas, which employ a range of cell references rather than a single number, as seen below.
The chart was created with a particular function in mind.
=POWER(A2:A11, B1:K1)This is a formula for an array. The first argument of the POWER function is for each cell from A2 to A11, and the second argument is for each cell from B1 to K1. If the function is put in cell B2, the results will be automatically inserted in each cell from B2 to K11 to create the table above.
Using Excel’s POWER Function In Calculations
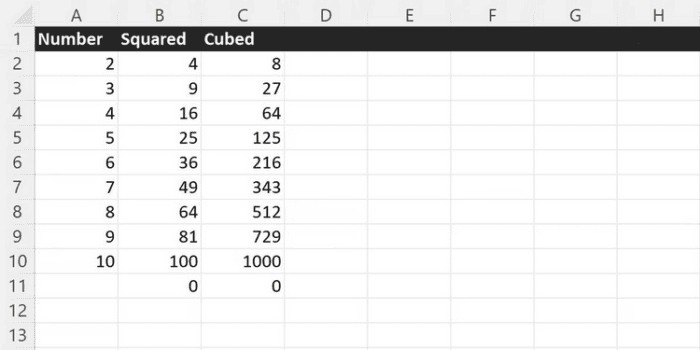
While the POWER function in Excel has limited use cases as a standalone function, it functions effectively as a basic square calculator.
=POWER(A2, 2)The values of B11 and C11 are significant in the preceding case. If the referred number to be raised to any power is an empty cell, it will be considered 0. As a result, the result of calling the POWER function on an empty cell is always 0.
Using POWER Function To Calculate Area Of A Circle In Excel
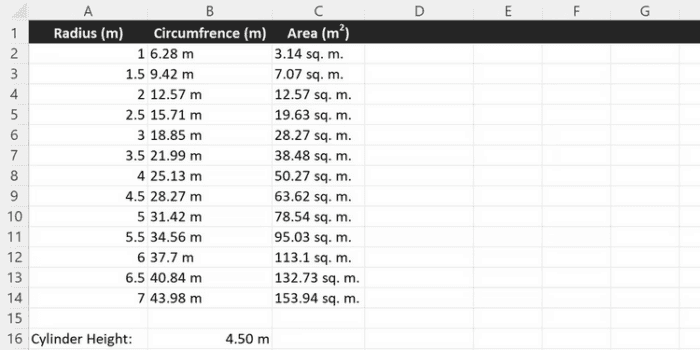
However, a considerably superior use case may be demonstrated with a little basic geometry. For example, we can calculate the area and circumference of a circle of changing radius by combining the POWER function with a mathematical formula. The circle’s area is equal to PI times the radius squared. In Excel, the formula may be quickly converted into an area calculator.
- Insert the radii of the circles you want to calculate into column A.
- Using a cell reference as the first argument and two as the second, the POWER function may be used to square the radius.
- PI may be guessed using 3.14, or it can be measured precisely using Excel’s PI function. But, first, multiply the PI function by the radius squared.
After you’ve created the first cell, C2, use the drag handle on the bottom right of the cell to fill the column.
=PI() * POWER(A2, 2)Finally, it is desirable to omit trailing decimal places for readability. There are many methods to change the decimal places in Excel. The ROUND function is the easiest solution in this case. The ROUND function in Excel may truncate results to a given number of decimal places. Use the following formula as the first argument to the ROUND function and the number of decimal places as the second.
=ROUND(PI() * POWER(A2, 2), 2)Calculating Volume Of A Cylinder In Excel
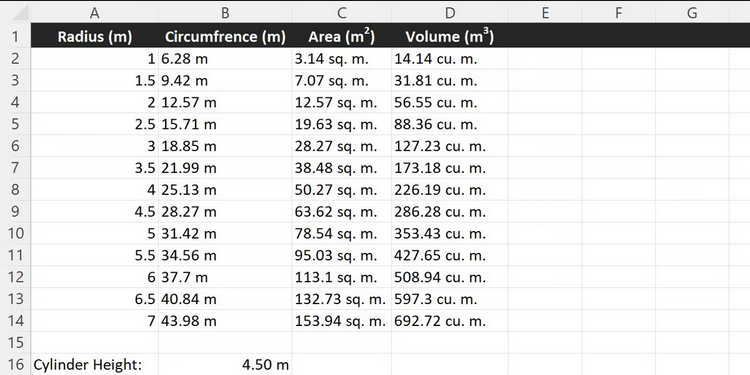
By adding a variable to the equation, you can calculate the volume of a cylinder. The volume of a cylinder is just the equation for the area of a circle multiplied by the cylinder’s height, h. For example, B16 in the new spreadsheet represents the cylinder’s height. With a little change, we can now multiply the same formula we used to find the area by the height.
=ROUND(PI() * POWER(A2, 2) * B$16, 2)Using POWER Function To Determine Arbitrary Roots In Excel
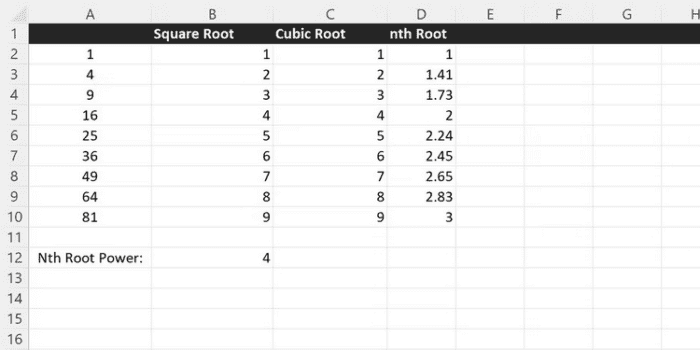
When creating complicated mathematical formulas for graphing, the POWER function is often employed. Such formulas are easy to depict using Excel’s built-in graph and chart capabilities. The POWER function may also be used to create an arbitrary root calculator. Excel has an SQRT function for determining square roots, but you’ll need to perform some more arithmetic for cubic roots or any root greater than 2.
Any root may be discovered by raising the number to one divided by the root number. For example, raising any number to 1/3 will provide a cubic root calculator. The POWER function in Excel helps you to find arbitrary roots quickly. When one divided by any number is used as the exponent, the POWER function is converted into a root finder for that number. For example, the function below will find the cubic root of the number A2.
=POWER(A2, 1/3)By referring to a cell in your workbook as the denominator in the second argument, you may create an arbitrary root-finding function by dividing one by any real number.
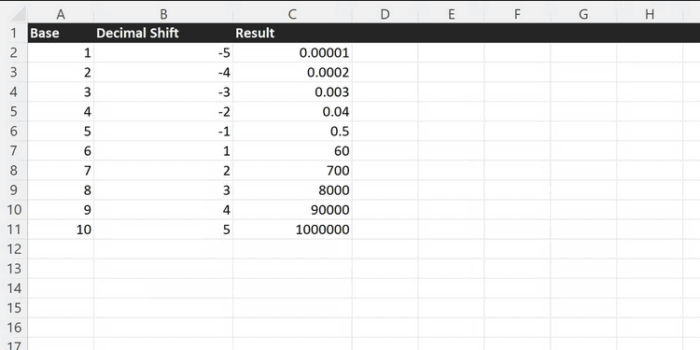
=ROUND(POWER(A2, 1/$B$12), 2)The POWER function may also be used to represent scientific notation easily. Displaying your numbers in scientific notation will help you to work with large or small values more readily. The scientific notation may be readily created using the POWER function on ten and either a positive or negative number.
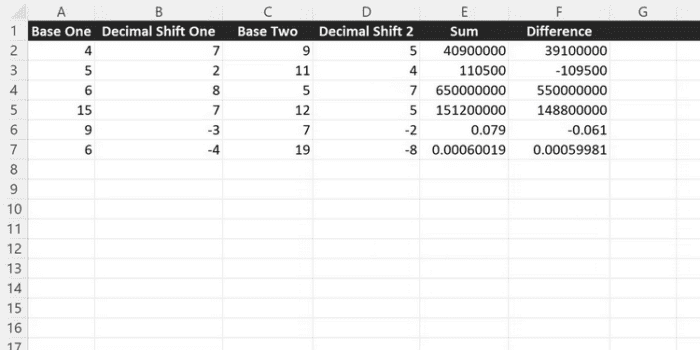
=A2 * POWER(10, B2)You may even use the POWER function in conjunction with a scientific calculator. Basic arithmetic may be performed on complex numbers while keeping them in an easy-to-read format.
=SUM(A2 * POWER(10, B2), C2 * POWER(10, D2))=(A2 * POWER(10, B2)) - (C2 * POWER(10, D2))Consider The Following:
Conclusion:
By alone, the POWER function may quickly find squares and cubes and arbitrary powers. It can quickly calculate root ranges by passing an array formula to create tables of exponents. Excel’s POWER function becomes quite handy when used with sophisticated mathematical formulas. The POWER function may solve various fundamental geometry issues, calculate arbitrary roots, and create graphs of complicated mathematical formulas. It may be used to create a basic scientific notation calculator. These characteristics make the POWER function essential knowledge for anybody working with complicated mathematical data.